Appendix E.Temperature Effects

If the ends of the structural member are free to expand or contract without restraint, strain changes can occur without any change in the stress reading. However, if the ends of a steel structural member are restrained by some semi-rigid medium, then any increase in temperature of the structural member will result in a buildup of compressive load related strain in the member, even though the actual strain would be tensile.

The strain gauge would accurately measure the magnitude of this temperature induced, compressive stress increase because the vibrating wire is not restrained from expansion, even though the member is restrained. Expansion would be indicated on the readout box by a decrease in the strain reading equal to the temperature-induced increase in compressive stress in the member.

These temperature-induced stresses can be separated from any external load-induced stresses by reading both the strain and the temperature of the gauge at frequent intervals. Take these readings during a period when the external loading from construction activity remains constant. When these strain changes are plotted against the corresponding temperature changes, the resulting graph shows a straight-line relationship, the slope of which yieldsa factor K_T. This factor can be used to calculate the temperature induced stress, as shown by the below equation:

 

  

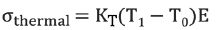
Equation 10: Temperature-Induced Stress

Subtract this from the observed apparent stress change using this equation:

 

 

Equation 11: Apparent Stress

Where:

B is the batch gauge factor.

E is Young’s modulus.

Use the following equation to determine the part of the stress change that is due to construction activity loads only:

 

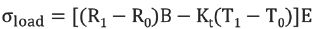
Equation 12: Load-Related Stress

Note that the correction factor, K_T, may change with time and with construction activity, as the rigidity of the restraint may change. It would then be a good idea to repeat the above procedure to calculate a new temperature correction factor.

If, for whatever reason, the actual strain of the steel member is required, (i.e., the change of unit length that would be measured by a dial gauge attached to the surface) you can arrive at this using this equation:

 

µε_actual = (R₁ – R₀) x B + (T₁ – T₀) x CF₁

Equation 13: Actual Strain

CF₁ is the coefficient of expansion of steel = 12.2 microstrains / °C. When the ends of the structural member are perfectly restrained then (R₁ – R₀)B the compressive strain induced by temperature change alone would be exactly canceled by (T₁ – T₀) x CF₁, the expansive strain and µε_actual would be zero.