5.Data Reduction

5.1Displacement Calculation

The basic units utilized by geokon for measurement and reduction of data from vibrating wire crackmeters are digits. Calculation of digits is based on the following equation:

      

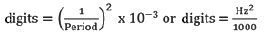
equation 1: Digits Calculation

To convert digits to displacement the following equation applies:  

D_uncorrected = (R₁ – R₀) x G x F

equation 2: Displacement Calculation

Where:

R₁ is the current reading.

R₀ is the initial reading, usually obtained at installation.

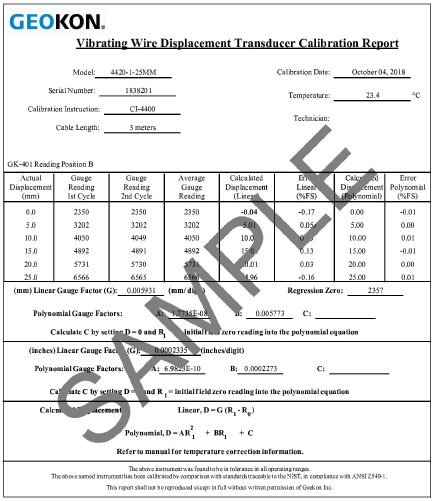
G is the gauge factor, usually millimeters or inches per digit (see Figure 12).

F is an optional engineering units conversion factor (see the table below).

table 4: Engineering Units Conversion Multipliers

For example, the initial reading R₀, at installation of a crackmeter is 2500 digits. The current reading, R₁, is 6000. The gauge factor is 0.006223 mm/digit. The displacement change is:

D_uncorrected = (6000 – 2500) x 0.006223 x +21.78

equation 3: Displacement Change

Note that increasing readings (digits) indicate increasing extension.

To use the polynomial gauge factors given on the calibration sheet, use the value of R₀ and Gauge Factors A and B with D set to zero to calculate the new value of C. Then substitute the new value of R₁ and use A, B, and the new value of C to calculate the displacement D.

12:    

Figure 12: Typical Crackmeter Calibration Sheet

5.2Temperature Correction

geokon’s vibrating wire displacement transducers have a small coefficient of thermal expansion. Correction may not be necessary in most cases. However, to achieve maximum accuracy, there are corrections that you can apply.

Use the following equation to provide thermal correction of the instrument:

D_corrected = G(R₁ – R₀) + K(T₁ – T₀) 

equation 4: Thermally-Corrected Displacement Calculation

Where:

R₁ is the current reading

R₀ is the initial reading

G is the linear gauge factor

T₁ is the current temperature

T₀ is the initial temperature

K is the thermal coefficient (see Equation 5)

 

Tests have determined that the thermal coefficient, K, changes with the position of the transducer shaft. The first step in the temperature correction process is determination of the proper thermal coefficient based on the following equation:

K = ((R₁ x M) + B) x G

equation 5: Thermal Coefficient Calculation

Where:

R₁ is the current reading

M is the multiplier, from Table 5

B is the constant, from Table 5

G is the linear gauge factor from the supplied calibration sheet.

table 5: Thermal Coefficient Calculation Constants

Consider the following example using a Model 4420-200 mm crackmeter:

R₀ = 4773 digits

R₁ = 4589 digits

T₀ = 20.3 °C

T₁ = 32.9 °C

G = 0.04730 mm/digit

K = (((4589 x 0.000396) – 0.4428) x 0.04730) = 0.065011

D_corrected = ((R₁ – R₀) x G) + ((T₁ – T₀) x K)

D_corrected = ((4589 – 4773) x 0.04730) + ((32.9 – 20.3) x 0.065011)

D_corrected = (–184 x 0.04730) + 0.819

D_corrected = –8.7032 + 0.819

D_corrected = –7.8842 mm

 

The temperature coefficient of the mass or member to which the crackmeter is attached should also be taken into account. Use the temperature coefficient of the mass or member, combined with the changes in temperature from initial to current readings, to determine thermal effects of the mass or member.

5.3Environmental Factors

Because the purpose of using a crackmeter is to monitor site conditions, factors which may affect these conditions should always be observed and recorded. Seemingly minor effects may have a real influence on the behavior of the structure being monitored and may give an early indication of potential problems. Some of these factors include, but are not limited to: blasting, rainfall, tidal levels, excavation and fill levels and sequences, traffic, temperature and barometric changes, changes in personnel, nearby construction activities, seasonal changes, etc.