Appendix D.Improving Calculated Pressure Accuracy
Most vibrating wire pressure transducers are sufficiently linear (± 0.2 % FS) that use of the linear calibration factor satisfies normal requirements. However, it should be noted that the accuracy of the calibration data, which is dictated by the accuracy of the calibration apparatus, is always ± 0.1% F.S.
This level of accuracy can be recaptured, even where the transducer is nonlinear, using a second order polynomial expression, which gives a better fit to the data then does a straight line. The polynomial expression has the form:
Pressure = AR2 + BR + C
equation 16: Pressure Calculation with Second Order Polynomial
Where:
R is the reading (digits channel B)
A, B, and C are coefficients
Figure 19 shows a typical calibration sheet of a transducer that has a very little nonlinearity. The figure under the “Linearity (%FS)” column is:
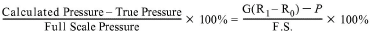
equation 17: “Linearity (%F.S.)” on Calibration Sheet
Note: The linearity is calculated using the regression zero for R0 shown on the sheet.
For example, from the typical sheet shown in Figure 19:
P= 210 kPa, G (R1 – R0) = −0.1192(7223 − 8983)
Gives a calculated pressure of 209.8 kPa, the error is 0.2 kPa.
Whereas the polynomial expression gives a calculated pressure of:
A (7223)2 + B (7223) + 1053 = 209.9 kPa
The actual error is only 0.1 kPa.
This is an insignificant improvement, however, where the nonlinearity is higher, for example ± 0.25% F.S., the improvement could be significant.
Note: If the polynomial equation is used it is important that the value of C, in the polynomial equation, be taken in the field, following the procedures described in Section 2.5. The field value of C is calculated by inserting the initial field zero readin into the polynomial equation with the pressure, P, set to zero.
If the field zero reading is not available, calculate C using the zero pressure reading on the calibration sheet. In the above example, the value of C would be derived from the equation:
0 = A(8981)2 + B(8981) from which C = +1053
equation 18: Calculating C Using the Zero Pressure Reading from the Cal Sheet
It should be noted that where changes of earth pressures are being monitored it makes little difference whether the linear coefficient or the polynomial expression is used.